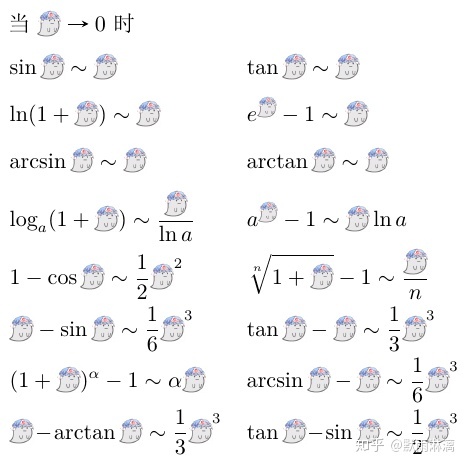等价无穷小

定义

设 $\lim_{x \to \Delta} f(x) = \lim_{x \to \Delta} g(x) = 0, \lim_{x \to \Delta} \dfrac{f(x)}{g(x)} = l$,

• 若 $l = 0$, 则 $f(x)$ 是 $g(x)$ 的高阶无穷小, 记作 $f(x) = o(g(x)) (x \to \Delta)$;
• 若 $l \neq 0$, 则 $f(x)$ 是 $g(x)$ 的同阶无穷小, 记作 $f(x) = O(g(x)) (x \to \Delta)$;
  • 若 $l = 1$, 则 $f(x)$ 是 $g(x)$ 的等价无穷小, 记作 $f(x) \sim g(x) (x \to \Delta)$;

k阶无穷小

若 $\lim_{x \to x_0} \alpha(x) = 0$, 且 $\exists c \neq 0, k > 0$, 使 $\lim_{x \to x_0} \dfrac{\alpha(x)}{(x-x_0)^k} = c$, 则当 $x \to x_0$ 时, $\alpha(x)$ 是k阶无穷小, $c(x - x_0)^k$ 为 $\alpha(x)$ 的主部 ($\alpha(x) = c(x - x_0)^k + o((x - x_0)^k)$)

警告

注意: $\alpha(x)$ 是k阶无穷小, 而不是 c阶无穷小

常见的等价无穷小替换

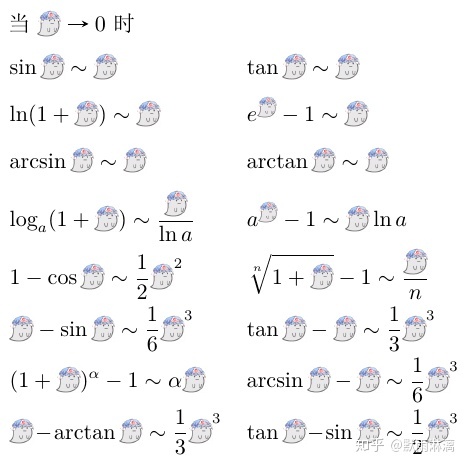常见的等价无穷小.jpg

警告

注意：

1. 加减法不能用等价无穷小替换
2. 替换必须保证前后都是无穷小(错误示范: $e^x \sim x + 1$)