直角坐标、极坐标、参数方程

直角坐标 $\to$ 极坐标

将直角坐标中的 $x, y$ 替换为 : $\begin{cases} x \to r\cos \theta \\ y \to r\sin \theta \end{cases}$

注意

注意: 需用 $r \geq 0$ 求出 $\theta$ 的取值范围（定义域）

极坐标 $\to$ 参数方程:

使用极坐标中的 $r(\theta)$ 替换该参数方程 : $\begin{cases} x = r(\theta) \cos \theta \\ y = r(\theta) \sin \theta \end{cases}$

极坐标 $\to$ 直角坐标（不一定成功）:

使用 $\begin{cases} r &= \sqrt{x^2 + y^2} \\ \sin \theta &= \dfrac{y}{\sqrt{x^2 + y^2}} \\ \cos \theta &= \dfrac{x}{\sqrt{x^2 + y^2}} \\ \tan \theta &= \dfrac{y}{x} \end{cases}$

常见极坐标/参数方程图像

• 摆线

  $$\begin{cases} x = a(\theta - \sin \theta) \\ y = a(1 - \cos \theta) \end{cases}$$

  
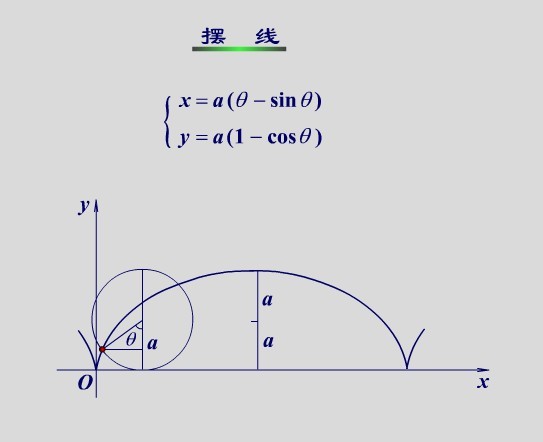
  摆线.jpeg
• 心脏线:

| $$\rho = 1 - \cos \theta$$
![心脏线1.png]] | $$\rho = 1 + \cos \theta$$
![[心脏线2.png](图片/心脏线1.png]] | $$\rho = 1 + \cos \theta$$
![[心脏线2.png) | | ------------------------------------------- | ------------------------------------------- | | $$\rho = 1 - \sin \theta$$
![心脏线3.png]] | $$\rho = 1 + \sin \theta$$
![[心脏线4.png](图片/心脏线3.png]] | $$\rho = 1 + \sin \theta$$
![[心脏线4.png) |

• 玫瑰线
  1. 三叶玫瑰线

| $$\rho = a \sin 3\theta$$
![三叶玫瑰线1.png]] | $$\rho = a \cos 3\theta$$
![[三叶玫瑰线2.png](图片/三叶玫瑰线1.png]] | $$\rho = a \cos 3\theta$$
![[三叶玫瑰线2.png) | | -------------------------------------------- | -------------------------------------------- |

• 双纽线

| $$\rho^2 = a^2 \cos 2\theta$$
![双纽线1.png]] | $$\rho^2 = a^2 \sin^2 \theta$$
![[双纽线2.png](图片/双纽线1.png]] | $$\rho^2 = a^2 \sin^2 \theta$$
![[双纽线2.png) | | ---------------------------------------------- | ----------------------------------------------- |

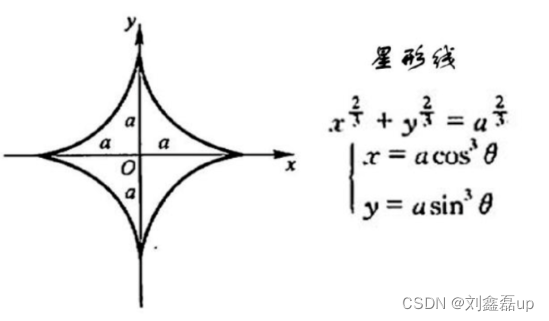
• 星形线